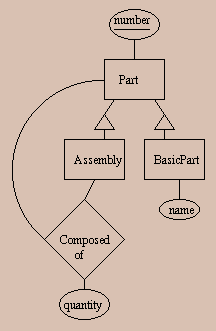
It represents ``parts explosion, in which any part is either a basic part, or an assembly consisting of some number of one or more subparts. For instance, a bicycle might be described as an assembly consisting of one frame and two wheels, while a frame is a basic part and a wheel is an assembly consisting of one tire, one rim, and 48 spokes.
- (a)
- Convert the E/R diagram to relations, using the strategy described in the text for going from E/R to relations.
- (b)
- Your answer to (a) should have several relations whose schemas are the same or one is a subset of the other. Do you want to retain all these relations? Justify your answer. Note: there can be more than one right answer; we are more interested in your reasoning than in ``yes'' or ``no.''
- (a)
- Convert the E/R diagram from Question 1 to an ODL description.
- (b)
- Then construct relations from your ODL, using the strategy for going from ODL to relations outlined in the text.
- (c)
- What differences, if any do you notice compared with your answer to 1(a)? Explain the differences or lack thereof.
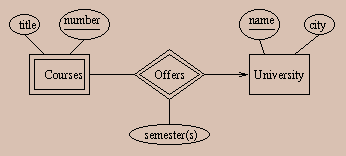
The intent of ``semester(s)'' is that this attribute is a code indicating which quarters or semesters the course is offered at that university. For example, for the related pair ``CS145'' and ``Stanford,'' the ``semester(s)'' would be ``fall and spring quarters.''
Convert this E/R diagram to relations, eliminating any redundant relations.
- (a)
- How many superkeys are there? Justify your answer.
- (b)
- Give two sets of functional dependencies that will make ABC and CD be the only keys. Your sets of FD's should each have the property that no proper subset of your FD's is equivalent to the full set; i.e., if you delete any FD, then the set of keys is something other than {ABC, CD}.
- (a)
- Give the set of FD's that hold for each of these two relations. You need not list every FD, but list enough so that all other FD's follow logically from the ones you give.
- (b)
- Are ABC and/or ABDEF in Boyce-Codd Normal Form? Justify your answer.