CS245 Winter 1999
due in class on Tuesday March 9
START OF ASSIGNMENT 7
PROBLEM 1
Consider the following two transactions:
T0: read(A);
read(B);
if (A = 0) then B = B + 1;
write(B);
T1: read(B);
read(A);
if (B = 0) then A = A + 1;
write(A);
Let the consistency requirement be (A = 0) OR (B = 0),
with A = B = 0 the initial values
(a) Show that every serial execution involving these two
transactions preserves the consistency of the database.
(b) Show a concurrent execution of T0 and T1 which produces a
nonserializable schedule
(c) Is there a concurrent execution of T0 and T1 which produces a
serializable schedule?
PROBLEM 2
Consider the following labeled precedence graph:
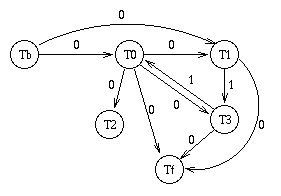 Is the corresponding schedule view-serializable? Explain your answer.
PROBLEM 3
(a) Give a *simple* schedule where (exactly) one transaction is not well
formed, and this causes the schedule to be non-conflict-serializable.
Show why your schedule is not conflict-serializable.
(b) Give a *simple* example of a non-legal schedule that is not
conflict-serializable. Show why your schedule is not conflict-serializable.
(c) Give a *simple* schedule where (exactly) one transaction is not two
phase, and this causes the schedule to be non-conflict-serializable.
Show why your schedule is not conflict-serializable.
PROBLEM 4
In a lock table, the system keeps a "group mode" that records the
"strongest" lock type of the transactions that have currently
locked an object. In particular, say object O is locked in
modes M1, ... Mj and let the group mode of O be GM(O).
Then, for any possible lock mode N,
(i) GM(O) and N are not compatible if and only if there is an
Mi element of {M1, ..., Mj} such that N and Mi are not
compatible; and
(ii) GM(O) and N are compatible if and only if for all Mi element of
{M1, ..., Mj}, N and Mi are compatible.
When a new lock request arrives, for lock mode N, the system can simply
check if N is compatible with GM(O),
instead of checking N against all locks currently held on object O.
Consider the multiple granularity locking mechanism (Section 9.6).
In each of sub-problems (a) through (f) below, the modes of currently
held locks on an object O are given. (For instance, in case (a),
object O is locked in mode IS by one transaction and in mode IX by
another.) For each case, give the group mode, if there is one.
(Be careful, some of the cases below are impossible! In those cases,
just say there is no group mode.)
(a) IS, IX
(b) IS, S
(c) IS, S, S
(d) IS, S, IX
(e) SIX, IS
(f) IX, X
END OF ASSIGNMENT 7
Is the corresponding schedule view-serializable? Explain your answer.
PROBLEM 3
(a) Give a *simple* schedule where (exactly) one transaction is not well
formed, and this causes the schedule to be non-conflict-serializable.
Show why your schedule is not conflict-serializable.
(b) Give a *simple* example of a non-legal schedule that is not
conflict-serializable. Show why your schedule is not conflict-serializable.
(c) Give a *simple* schedule where (exactly) one transaction is not two
phase, and this causes the schedule to be non-conflict-serializable.
Show why your schedule is not conflict-serializable.
PROBLEM 4
In a lock table, the system keeps a "group mode" that records the
"strongest" lock type of the transactions that have currently
locked an object. In particular, say object O is locked in
modes M1, ... Mj and let the group mode of O be GM(O).
Then, for any possible lock mode N,
(i) GM(O) and N are not compatible if and only if there is an
Mi element of {M1, ..., Mj} such that N and Mi are not
compatible; and
(ii) GM(O) and N are compatible if and only if for all Mi element of
{M1, ..., Mj}, N and Mi are compatible.
When a new lock request arrives, for lock mode N, the system can simply
check if N is compatible with GM(O),
instead of checking N against all locks currently held on object O.
Consider the multiple granularity locking mechanism (Section 9.6).
In each of sub-problems (a) through (f) below, the modes of currently
held locks on an object O are given. (For instance, in case (a),
object O is locked in mode IS by one transaction and in mode IX by
another.) For each case, give the group mode, if there is one.
(Be careful, some of the cases below are impossible! In those cases,
just say there is no group mode.)
(a) IS, IX
(b) IS, S
(c) IS, S, S
(d) IS, S, IX
(e) SIX, IS
(f) IX, X
END OF ASSIGNMENT 7
 Is the corresponding schedule view-serializable? Explain your answer.
PROBLEM 3
(a) Give a *simple* schedule where (exactly) one transaction is not well
formed, and this causes the schedule to be non-conflict-serializable.
Show why your schedule is not conflict-serializable.
(b) Give a *simple* example of a non-legal schedule that is not
conflict-serializable. Show why your schedule is not conflict-serializable.
(c) Give a *simple* schedule where (exactly) one transaction is not two
phase, and this causes the schedule to be non-conflict-serializable.
Show why your schedule is not conflict-serializable.
PROBLEM 4
In a lock table, the system keeps a "group mode" that records the
"strongest" lock type of the transactions that have currently
locked an object. In particular, say object O is locked in
modes M1, ... Mj and let the group mode of O be GM(O).
Then, for any possible lock mode N,
(i) GM(O) and N are not compatible if and only if there is an
Mi element of {M1, ..., Mj} such that N and Mi are not
compatible; and
(ii) GM(O) and N are compatible if and only if for all Mi element of
{M1, ..., Mj}, N and Mi are compatible.
When a new lock request arrives, for lock mode N, the system can simply
check if N is compatible with GM(O),
instead of checking N against all locks currently held on object O.
Consider the multiple granularity locking mechanism (Section 9.6).
In each of sub-problems (a) through (f) below, the modes of currently
held locks on an object O are given. (For instance, in case (a),
object O is locked in mode IS by one transaction and in mode IX by
another.) For each case, give the group mode, if there is one.
(Be careful, some of the cases below are impossible! In those cases,
just say there is no group mode.)
(a) IS, IX
(b) IS, S
(c) IS, S, S
(d) IS, S, IX
(e) SIX, IS
(f) IX, X
END OF ASSIGNMENT 7
Is the corresponding schedule view-serializable? Explain your answer.
PROBLEM 3
(a) Give a *simple* schedule where (exactly) one transaction is not well
formed, and this causes the schedule to be non-conflict-serializable.
Show why your schedule is not conflict-serializable.
(b) Give a *simple* example of a non-legal schedule that is not
conflict-serializable. Show why your schedule is not conflict-serializable.
(c) Give a *simple* schedule where (exactly) one transaction is not two
phase, and this causes the schedule to be non-conflict-serializable.
Show why your schedule is not conflict-serializable.
PROBLEM 4
In a lock table, the system keeps a "group mode" that records the
"strongest" lock type of the transactions that have currently
locked an object. In particular, say object O is locked in
modes M1, ... Mj and let the group mode of O be GM(O).
Then, for any possible lock mode N,
(i) GM(O) and N are not compatible if and only if there is an
Mi element of {M1, ..., Mj} such that N and Mi are not
compatible; and
(ii) GM(O) and N are compatible if and only if for all Mi element of
{M1, ..., Mj}, N and Mi are compatible.
When a new lock request arrives, for lock mode N, the system can simply
check if N is compatible with GM(O),
instead of checking N against all locks currently held on object O.
Consider the multiple granularity locking mechanism (Section 9.6).
In each of sub-problems (a) through (f) below, the modes of currently
held locks on an object O are given. (For instance, in case (a),
object O is locked in mode IS by one transaction and in mode IX by
another.) For each case, give the group mode, if there is one.
(Be careful, some of the cases below are impossible! In those cases,
just say there is no group mode.)
(a) IS, IX
(b) IS, S
(c) IS, S, S
(d) IS, S, IX
(e) SIX, IS
(f) IX, X
END OF ASSIGNMENT 7