| CS245A PROBLEM SET #2
Due by 5pm, Tuesday, January 27, 1998.
4 problems, equal credit. 100 pts.
|
Problem 1: B+-trees and B-trees
The Megatron 2000 DBMS has the following characteristics:
- 4 KB fixed-size blocks
- 8-byte pointers
- 16-byte block headers
- i)
- We want to build a B+tree index on a search key that is 12 bytes long.
Compute the maximum number of records we can index with a 3-level B+tree (2 levels plus
the root.)
- ii)
- B-trees (they are pronounced "B trees", not "B minus trees")
are a variation of B+trees. The main distinguishing characteristic
is that a B-tree allows a search key value to appear only once. To be able to do that,
non-leaf index nodes have to include a record pointer to the record associated to the
search key (only leaf nodes point to data in B+trees).
For a more detailed presentation of B-trees, please see the textbook, pp 356-358.
-
We want to build a B-tree index on the same search-key as in i).
Again compute the maximum number of records we can index with a 3-level B-tree.
Which of the two schemes allows us to index more records?
What conclusion can you draw from this comparison about the performance of the
two indexing schemes?
Problem 2: B+tree insertions and deletions
Consider the following B+tree.
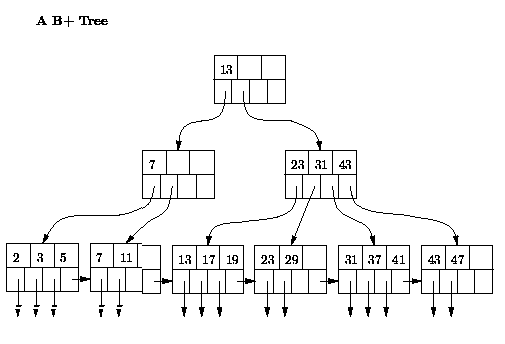
Show the B+tree that results after inserting (in the given order) 36, 18, 40.
From that resulting B+tree we delete (in the given order) 43, 13, 7.
What is the resulting final B+tree?
Problem 3: Record organization - Repeating fields
A relational database holds a relation A whose records have the following
schema:
- A record header 4 bytes long
- 2 fixed-length fields 8 bytes long each
- 2 fixed-length fields 12 bytes long each
- 1 fixed-length field f of length 8 bytes that is a repeating field.
Specifically, 30% of the records have 0-2 f such fields, 50% of the records have
3-6 f fields and the rest have 7 or 8 f fields.
Within each range, the number of f fields in each record follows the uniform
distribution.
Consider the following two ways of laying out the records of relation A on disk.
- a)
- One way is to treat them as fixed-length records,
by allocating for each record the maximum necessary amount of space. The main drawback
of this approach is obviously the wasted space (unused space inside a record is
wasted space).
- b)
- Another way is to split the record in a fixed-length and a variable-length part.
The fixed length part would then include a pointer to the variable-length
part, that would reside on a different block.
Please answer the following questions
- i)
- Assume that we are using the Megatron 2000 DBMS from Problem 1 to store
our relation. Also assume that the relation is stored in as few blocks as possible.
What is the average percentage of empty space per block for a)?
What is it for b) (assuming the variable-length part is
stored with no wasted space)?
Spanning of records is not allowed.
- ii)
- Queries to the database are of the (very simple) form "Give me attribute a of
the record pointed to by r" (where r is a record pointer).
Assume only 25% of all queries to the relation A
need to access the repeating fields; the rest just need to access the fixed-length part
of a record. What is the average number of disk accesses
needed to fetch a record of A under schemes a) and b)?
Problem 4: Block reorganization
We have a 1MB file consisting of records 256 bytes long and
we want to store it as a sequential file
with a sparse index on the primary key.
The index points to the first record on each block of the file.
The size of each block is 8KB and the block header is 16 bytes.
We know there will be insertions (but no deletions) to the file.
It is therefore better to leave empty space in
each block so that the file has space to grow.
We initially use only 70% of each block to store records.
When a block is full and we need to add a record to it, we add an overflow
block and point to it from the "primary" block. We then redistribute the blocks so that
half of them remain on the primary block and half are pushed to the overflow block.
The index is not updated, i.e., there is
still just one pointer to the first record of the "primary" block.
Let us assume there are 5 update operations per minute, and that each one
tries to insert 1 record to a primary block. Updates are uniformly distributed among blocks.
Let us also assume that we are querying the database using the primary key.
The query is simply "fetch the record with key k."
All queries search for existing keys; we query with the same frequency
about all existing keys.
Assume the sparse index can be kept in main memory.
- a)
- What is the number of disk accesses needed to answer a query initially?
- b)
- After how much time will the average number of disk accesses to locate a record
become higher than 1.5?
Last modified: Mon Jan 19 18:57:18 PST